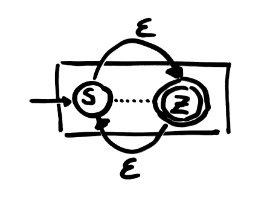
Automata
An automata is a 5 component object where:
- T is the alphabet
- Q is a set o states
- S is the initial state
- Z is the final state
- δ is the state transition function
Non-deterministic Automata (AND)
A non-deterministic automata, its an automata in which the state transition function is given a certain state and a symbol of the alphabet. As a result it shall give us a set of states.
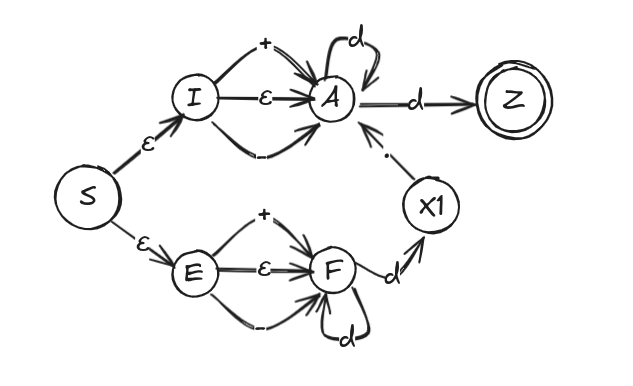
GSR to AND
Let’s consider the following GSR:
S → I | E
I → A | ’+’ A | ’-’ A
A → d Z | d A
E → ’+’ F | ’-’ F | F
F → d F | d X1
X1 → ’.’ A
Z → ε
Analysing it we can determine the following AND:
Deterministic Automata (AD)
A deterministic automata is an automata in which the state transition function is given a certain state and a symbol of the alphabet. As a result it gives back a state.
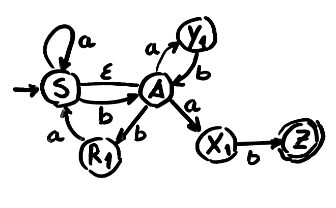
AND to AD
Let take into account the following grammar and automata:
S → A | a S | b A
A → a X1| a Y1| b R1
X1 → b Z
Y1 → b A
R1 → a S
Z → ε
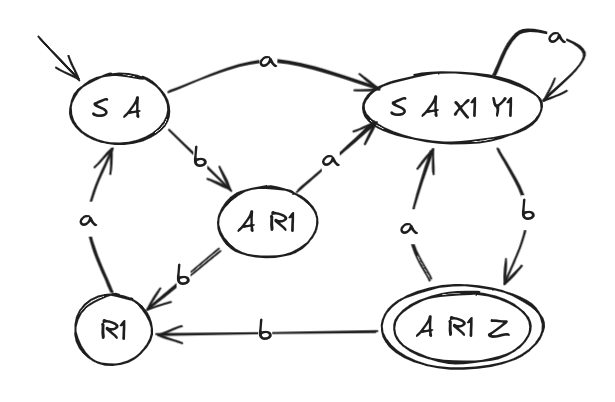
A viable method to transform an AND to an AD is using a table:
| State | a | b |
|---|---|---|
| S,A | S,A,X1,Y1 | A,R1 |
| S,A,X1,Y1 | S,A,X1,Y1 | A,R1,Z |
| A,R1 | X1,Y1,S,A | R1 |
| A,R1,Z | X1,Y1,S,A | R1 |
| R1 | S,A |
Having this table we can reproduce the following AD automata:
Regex to AND
A thing about regular expressions is that we can also convert them into AND automata.
Here are the following
- e = φ
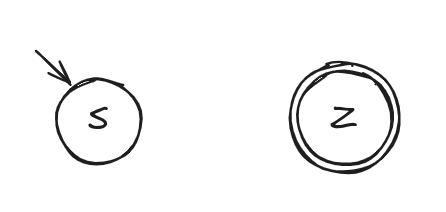
- e = ε
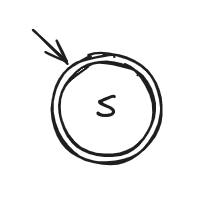
- e = a
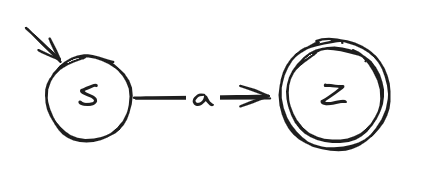
- e = p + q (p and q are regular expressions)
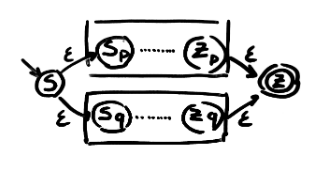
- e = p . q
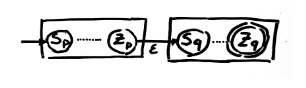
- e = p+
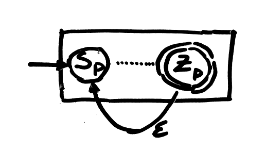
- e = p*